Grandezas em corrente alternada
Potências ativa, reativa e aparente: a definição quantitativa das potências são caraterizadas pela multiplicação das grandezas relativas às tensões e correntes. Ao longo dos últimos quase cem anos as definições em regime não senoidal foram sendo aperfeiçoadas culminando nas definições da IEEE 1459 (IEEE Standard Definitions for the Measurement of Electric Power Quantities Under Sinusoidal, Nonsinusoidal, Balanced, or Unbalanced Conditions”. Este assunto já foi tratado nesta coluna e está disponível nos links: https://www.osetoreletrico.com.br/var-e-var-a-medicao-da-potencia-reativa-e-as-outras-em-regime-nao-senoidal-parte-2/ e https://www.osetoreletrico.com.br/var-e-var-a-medicao-da-potencia-reativa/
Em regime senoidal, onde as formas de onda de tensão e corrente podem ser consideradas (ou aproximadas para senoides com baixa distorção de tensão), as expressões abaixo definem as potências ativa, reativa e aparente:
Potência aparente “S” expressa em VA (maiúsculos) e seus múltiplos (kVA, MVA):
S= V*I em sistemas monofásicos (5)
ou S=raiz(3)*V*I ( em sistemas trifásicos) (6)
Potência ativa: “P” expressa em W (maiúsculo) e seus múltiplos (kW, MW):
P= V*I* FP em sistemas monofásicos (7)
ou P=raiz(3)*V*I*FP ( em sistemas trifásicos) (8)
A potência reativa “Q” expressa em var (minúsculo) e seus múltiplos (kvar, Mvar):
Q=raiz(S2-P2) considerando-se S e P em sistemas trifásicos ou monofásicos (9)
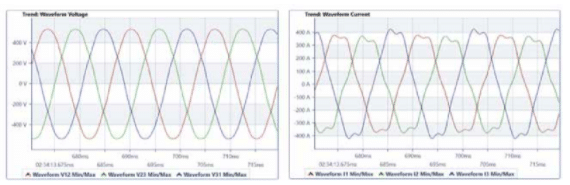
O ângulo φ representa a defasagem entre os fasores de tensão e corrente e naturalmente depende da carga, podendo ser identificado tanto na análise da forma de onda de tensão e corrente (ver Figura 1 da primeira parte, reproduzida novamente a seguir) como no bem conhecido triangulo das potências de valores eficazes (rms) apresentado na Figura 2.
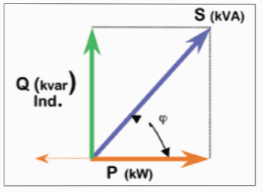
As relações trigonométricas, relacionadas ao ângulo φ são assim definidas:
P= V*I*cos φ (10) e P= raiz(3) V*I*cos φ (11)
Q= V*I*sen φ (12) e Q= raiz(3) V*I*sen φ (13)
P=S*cos φ (14) e Q = S* sen φ (15)
φ = arco tangente (Q/P)