
A Curva Média de Resistividades Aparentes: parte 1
Este artigo apresenta as justificativas para que, com base em um conjunto de curvas de resistividades aparentes obtidas a partir de uma campanha de sondagens elétricas verticais (com arranjo de Wenner ou de Schlumberger), seja calculada uma curva média geométrica de resistividades aparentes, que será invertida para a obtenção do modelo geoelétrico correspondente.
A adoção da curva média geométrica como representativa do solo médio de uma área onde vai ser construído um sistema de aterramento foi uma das novidades da última revisão da norma NBR 7117, publicada em novembro de 2020.
A curva média de resistividades aparentes é aquela construída a partir da média geométrica dos valores de resistividades aparentes obtidos para cada espaçamento entre eletrodos. Antes de se proceder ao cálculo da curva média, há que se eliminar os valores extremos (outliers), que são valores atípicos ou discrepantes no conjunto de dados disponível, que fogem ao padrão que caracteriza a distribuição do parâmetro de interesse. A identificação dos outliers é uma etapa essencial do processamento da base de dados disponível.
Uma forma de filtrar a base de dados pode adotar a simples eliminação dos valores que extrapolarem as décadas de resistividades dominantes na sondagem, quando estes valores discrepantes forem poucos com relação ao universo de valores disponíveis. Alternativamente, pode-se proceder a uma filtragem baseada no cálculo do desvio padrão dos logaritmos das resistividades aparentes medidas, com a eliminação dos valores situados fora da faixa de ± um ou dois desvios padrão (a critério do projetista). Ambas as técnicas aqui mencionadas são previstas pela NBR 7117/2020, constituindo também novidades desta última revisão da norma.
Um conjunto de valores pode ter diferentes médias, conforme o critério de cálculo utilizado:
A Figura 1 apresenta graficamente as quatro primeiras médias, entre os valores A e B, onde pode-se observar que:
A média quadrática, também conhecida como valor eficaz (RMS), é a maior das quatro médias por dar um peso mais elevado aos valores mais altos quando os eleva ao quadrado. A Tabela 1 apresenta as expressões para as médias simples (não ponderadas) de n sondagens de mesmo espaçamento.
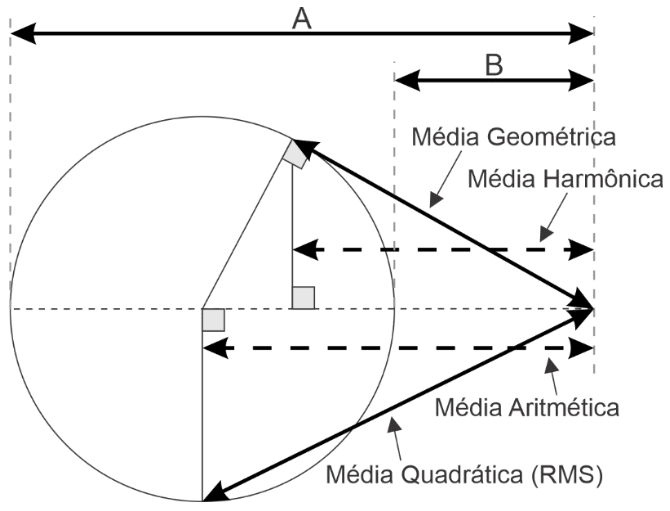
Figura 1: expressão gráfica das médias entre os valores A e B – quadrática, aritmética, geométrica e inversa.

Tabela 1: expressões para as médias não ponderadas de n valores de resistividades aparentes (ρ), onde média quadrática (RMS) > média aritmética > média geométrica > média harmônica.
A Curva Média de Resistividades Aparentes – Ponto de Vista Estatístico
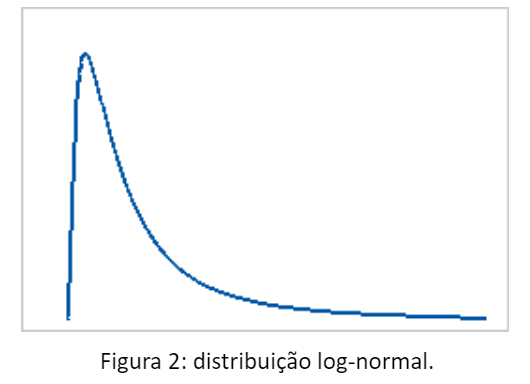
O solo é uma estrutura complexa com várias fases – componentes sólidos (minerais), líquidos e gasosos (contidos nos poros dos sedimentos e das rochas). Diferentes tipos de rochas apresentam diferentes características como: porosidade, permeabilidade, compactação, constituição química, conteúdo fluido etc. Em geociências a maioria destes parâmetros têm distribuições assimétricas positivas, e assim ocorre com a resistividade elétrica. Diz-se que a distribuição log-normal é o normal da geologia, sendo uma distribuição assimétrica com cauda que se estende para a direita (Figura 2).
A resistividade elétrica em um determinado terreno apresenta normalmente um significativo intervalo de valores, que normalmente abrange pelo menos duas décadas. A lei de Archie correlaciona a condutividade elétrica das rochas com a sua porosidade e com a saturação de fluidos nos seus poros. Esta lei revela que a resistividade elétrica de uma rocha é definida basicamente por um produto de parâmetros relacionados com a sua constituição, tais como, porosidade, fração de poros saturados e resistividade do fluido contido nesses poros. A distribuição log-normal é associada a parâmetros que abrangem mais de uma década no espaço log-log e que podem ser expressos pelo produto de diversos outros parâmetros. Fica evidente, portanto, que a distribuição log-normal aplica-se ao parâmetro resistividade elétrica.
Paulo Edmundo da Fonseca Freire é engenheiro eletricista e Mestre em Sistemas de Potência (PUCRJ). Doutor em Geociências (UNICAMP) e membro do CIGRE e do COBEI, também atua como diretor da Paiol Engenharia.