Conceitos básicos de eletrotécnica aplicada – 7ª parte Cargas das instalações e linearidade – cargas não lineares e fator de potência (continuação)

Ordem harmônica

Cada um dos sinais senoidais apresentados na edição anterior compõe o sinal “soma” e pode ser representado pela “ordem harmônica”, que é a relação da frequência do sinal pela frequência fundamental. Em um sistema elétrico de corrente alternada, 60 Hz, um sinal (corrente ou tensão) de 300 Hz é considerado como de 5ª harmônica, o de 420 Hz de 7ª harmônica e assim por diante. De forma a facilitar a representação e entendimento destes sinais, a representação mais utilizada é convencionalmente feita com a utilização do histograma apresentado na Figura 1. Nas abscissas são informadas não exatamente as frequências das correntes harmônicas, mas sim o número inteiro múltiplo que estas frequências guardam em relação à frequência fundamental, ou as ordens harmônicas. Assim o número 3 é relativo à frequência de 180 Hz (3ª harmônica) e o 5 é relativo a 5ª harmônica, 300 Hz.

Esse número relativo à frequência harmônica é utilizado como índice do sinal que se deseja representar. A grandeza I₅= 17A significa que a corrente eficaz (rms) de 5ª harmônica (em frequência de 300 Hz) é de 17 ampères. Concluindo, a referência a uma componente harmônica de ordem “n” significa que se está tratando de um sinal de tensão ou corrente em frequência “n.f”, em que f é a frequência fundamental.

Representação de um sinal:

O sinal “soma” da figura 2 da edição passada (i(t)), que é o sinal total distorcido é definido pela série de Fourier como a soma dos outros sinais senoidais. A expressão geral da Série de Fourier pode ser representada para um determinado sinal de corrente como:

i(t)=I_dc+I₁.sen(ωt+φ₁)+I₂.sen(2ωt+φ₂)+I₃.sen(3ωt+φ₃)+…. …… + I_h.sen(hωt+ φ_h)

em que:

I_dc é a componente de corrente contínua do sinal;

I_h (h=1,2,3…) é a máxima corrente (ou corrente de pico) na frequência harmônica “h”;

φ_h (h=1,2,3…) são os ângulos de defasamento de cada harmônica.

Na Figura 2 estão presentes as correntes harmônicas de ordem 3 e 5, além do sinal de corrente fundamental.

i(t)= I₁.sen(ωt+φ₁)+I₃.sen(3ωt+ φ₃) + I₅.sen(5ωt+ φ₅)

O valor máximo da corrente I1 será 81*√2 A (como cada um dos sinais que compõe o sinal distorcido é senoidal).

Imax_fund=√2*I1

A mesma metodologia não vale para o sinal soma que não é senoidal.

i(t)= 114.sen(ωt)+41.sen(3ωt)+24.sen(5ωt);

em que ω= 2.∏.f, sendo f a frequência fundamental, 60 Hz.

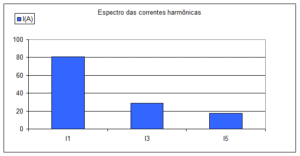
Outra forma usual de representação é a de quantificar cada harmônica em valores percentuais relativos ao valor da corrente fundamental. Assim o espectro harmônico formado pela terceira harmônica de 29 A e quinta harmônica de 17 A, pode ser representado conforme figuras 3 e 4

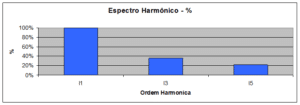
Da mesma forma podem ser representados os sinais de tensão harmônica.

Corrente eficaz do sinal harmônico

O valor eficaz de um sinal harmônico (tensão ou corrente) é calculado pela raiz das somas quadráticas dos valores eficazes de cada um dos sinais. Assim, a corrente eficaz de um sinal com componentes de correntes fundamental, segunda, terceira, quarta, quinta e outras harmônicas será:

Irms =

Analogamente, o valor eficaz do sinal tensão será:

Vrms =

Assim, o sinal de corrente apresentado na tabela 7.1 terá como valor eficaz:

I_rms = = 87,7 A

Resultando que a corrente eficaz (I_rms) será aproximadamente 8% superior à corrente fundamental (I₁).

Distorção total de um sinal harmônico

Com base no espectro das diversas componentes (corrente ou tensão) de um sinal harmônico, podem-se estabelecer os indicadores Distorção Harmônica Total de Tensão e de Corrente.

 A literatura e referências internacionais tratam a grandeza distorção harmônica total por THD (Total Harmonic Distortion), sendo THDI a distorção harmônica total de corrente e THDV de tensão. A norma ANEEL-Prodist módulo 8 trata esses indicadores por DHT (distorção harmônica total), DTT de “distorção total de tensão”.

Por uma questão de simplificação e adequação à terminologia utilizada nos instrumentos de medidas elétricas, trataremos estes indicadores por THDI e THDV, contrariando nesse caso as referências oficiais nacionais.

A definição da distorção total de um sinal é originada da raiz quadrada da soma quadrática das componentes harmônicas, definida como a raiz quadrada da soma dos quadrados dos sinais, relacionada ao valor do sinal na frequência fundamental. As expressões a seguir ilustram a distorção harmônica total de um sinal de corrente

ou ainda:

Continua na próxima edição.