Modelos de solos homogêneos

Solos homogêneos não existem na natureza. Qualquer método de redução de uma estrutura de subsuperfície a um modelo homogêneo está associada a uma incerteza básica – não existe solo homogêneo que, seja capaz de reproduzir a resistência de uma malha de aterramento e, simultaneamente, os gradientes de tensão na superfície do solo, o que significa tensões de passo e de toque. A descaracterização do modelo resulta na impossibilidade de calcular de forma adequada os parâmetros desejados.

Isto posto, há que se lembrar que metodologias de cálculo simplificado de malhas de aterramento requerem um valor único de resistividade do solo. Para o cálculo deste parâmetro, o Anexo E da IEEE-80/2013 propõe duas alternativas: média aritmética dos valores da curva média, ou média aritmética dos valores máximo e mínimo de resistividades.

Aplicando a primeira opção a uma curva média que abranja o conjunto de espaçamentos do arranjo de Wenner até 32 m, tem-se:

ρ(médio)=a 1m+a 2m+a 4m+a 8m+a 16m+a (32m)6

A segunda opção pode ser assim equacionada: (méd. extremos)=(ρmín.+ρmáx.)/2.

De acordo com a IEEE-80, estes critérios de cálculo foram obtidos com base em simulações de modelos de solo com duas camadas em que a diferença de resistividades é moderada. Pelo exemplo do Anexo E, que utiliza valores baixos de resistividades aparentes, uma diferença moderada é inferior a 4x entre os valores máximo e mínimo de resistividades aparentes. As simulações mencionadas pela IEEE-80 para validar estes modelos utilizaram malhas de pequeno porte em solos de baixas resistividades, da ordem ou inferiores a 250 Ωm.

Pelo 1º método, diferentes estruturas geoelétricas podem resultar em um mesmo modelo de solo, pois em uma média, a ordem dos fatores não altera o resultado; porém, a ordem das camadas geoelétricas certamente vai ter impacto no desempenho da malha.

Para a 2ª alternativa, a IEEE-80 estabelece que a expressão é válida se a malha tiver hastes e se elas atingirem uma camada com a resistividade média calculada (exigência que limita drasticamente a aplicação desta alternativa). Ora, para se determinar se as hastes da malha atingem uma camada de solo com a mesma resistividade da média entre os extremos, há que se produzir um modelo de solo estratificado em camadas (1D) e depois verificar se a exigência é atendida. Ora, se já se tem a geometria da malha e o modelo de solo 1D, então é melhor usar um software adequado e concluir o projeto, sem as incertezas de uma modelagem extremamente simplificada e altamente questionável.

A norma NBR-15751 (Aterramento de Subestações) está sendo revisada, e faz-se necessário o estabelecimento de uma metodologia de cálculo de modelos de solo uniforme, naturalmente, alertando para as restrições da sua aplicação.

A proposta mais simples é a adoção da primeira alternativa acima, porém, utilizando a média geométrica dos valores da curva média geométrica de resistividades aparentes, que abranja o conjunto de espaçamentos do arranjo de Wenner, com uma abertura AB compatível com a diagonal do terreno a ser modelado. Estas premissas visam a coerência com os critérios da NBR-7117/2020, que estabelece que as resistividades do solo têm distribuição log-normal.

Para um terreno com diagonal máxima de 70 m, por exemplo, tem-se:

ρ(médio)=6a (1m)×a (2m)×a (4m)×a (8m)×a (16m)×a (24m)

Cabe observar que este método está sujeito à mesma crítica já feita ao método proposto pela IEEE-80, uma vez que diferentes estruturas geoelétricas podem resultar em um mesmo modelo de solo, pois a ordem dos fatores continua não alterando a média, porém, a ordem das camadas geoelétricas certamente vai ter impacto no desempenho da malha de aterramento.

Para contornar esta restrição do método, propõe-se o cálculo da resistividade aparente média por meio da média geométrica das resistividades de cada espaçamento, porém, ponderadas por pesos, que de certa forma, reflitam a sequência das camadas. A resistividade média geométrica ponderada pode ser calculada em função dos valores de resistividade aparente para cada espaçamento AB (ρ_AB) e do peso atribuído à cada abertura AB (w_AB):

(a)=ei=1nABi i=1nwABi

Considerando que as malhas de aterramento estão sempre enterradas em profundidades rasas, é de se esperar que as camadas mais rasas do solo, onde é maior a densidade de corrente elétrica que flui da (ou para a) malha, devem ter um peso maior do que as camadas mais profundas.

Pode-se então estabelecer duas alternativas de pesos: o inverso da abertura de sondagem AB, e o logaritmo deste parâmetro. A Tabela 1 revela que o logaritmo é um peso mais adequado, pois o parâmetro AB tem uma variação em progressão geométrica, e o seu uso tornaria irrelevantes as sondagens de maiores aberturas.

Tabela 1: espaçamentos AB e respectivos logaritmos.

A resistividade média geométrica ponderada para uma dada curva de resistividades aparentes pode ser então assim calculada:

(a)=ei=1nABi i-1n1/logABi

Para o terreno com diagonal máxima de 70 m acima exemplificado, o valor a ser exponenciado para a obtenção da resistividade média geométrica ponderada pode ser assim calculado:

ln médio =ln3m0,48+ln6m0,78+ln12m1,08+ln24m1,38+ln48m1,68+ln72m1,8610,48+10,78+11,08+11,38+11,68+11,86 

Esta metodologia de cálculo de modelo de solo homogêneo tem as seguintes restrições:

• Diferença entre os valores máximo e mínimo de resistividades aparentes inferior a 4x;
• Curva média de resistividades aparentes característica de um solo de duas camadas (com apenas uma inflexão, para cima ou para baixo);
• Malha de pequeno porte (diagonal ≤ 70 m), em solo de baixa resistividade (≤ 250 Ωm).

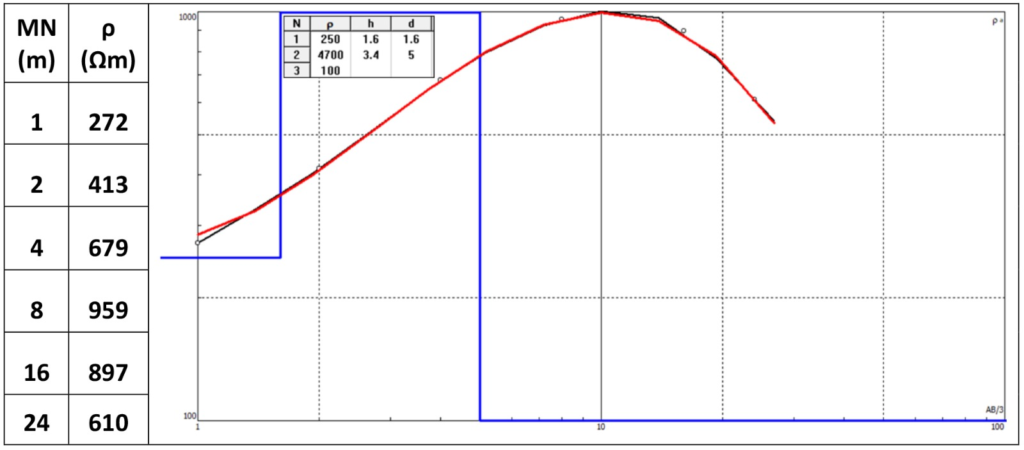
A aplicação a um caso real exemplifica bem a metodologia de cálculo do modelo de solo uniforme proposta. A Tabela 2 apresenta uma curva média geométrica de resistividades aparentes calculadas a partir de uma campanha de sondagens Wenner para o projeto de uma UFV GD. Esta curva média atende ao critério de diferença entre os valores máximo e mínimo de resistividades aparentes inferior a 4x; porém, não atende ao critério de solo de dupla camada e, portanto, uma malha de aterramento neste solo não poderia ser dimensionada por meio do método simplificado.

O cálculo do valor médio geométrico das seis resistividades aparentes desta curva resulta em 585 Ωm. Para exemplificar a aplicação do método alternativo de cálculo do modelo de solo uniforme, a resistividade média ponderada, conforme proposto, resulta em um valor médio de 475 Ωm, um pouco inferior à média geométrica simples, porque leva em conta o peso das resistividades aparentes mais baixas das camadas superficiais do solo, onde a malha está enterrada.

Figura 1: curva média geométrica de resistividades aparentes calculadas a partir de uma campanha de sondagens Wenner para o projeto de uma UFV GD, e modelo geoelétrico de 3 camadas correspondente.